Introduction to Fast Marching

The FM algorithm was introduced by J. Sethian in 1996 and is a numerical algorithm that approximates the viscosity solution of the Eikonal equation which represents, among other,
The FM method is used to solve the Eikonal equation and is very similar to the Dijkstra algorithm that finds the shortest paths on graphs, though it is applied to continuous media.

Fast Marching and Motion Planning

To get a Motion Planner for mobile robots with desirable
properties, such as smoothness and safety, we can think of
attractive potentials. In Nature, there are phenomena with a
similar behaviour, e.g., the electromagnetic waves. If there
is an antenna in the goal point that emits an electromagnetic
wave, then the robot can drive to the destination by tracing
the waves back to the source. In general, the concept of
electromagnetic waves is especially interesting, since the potential and its associated vector field have the good properties
desired for the trajectory, such as smoothness and the absence
of local minima.

This attractive potential still has some problems. The most
important one that typically arises in mobile robotics, is
that optimal motion plans may bring robots too close to
obstacles or people, which is not safe. To obtain a safe
path, it is necessary to add a component that repels the robot
from obstacles. In addition, this repulsive potential and its
associated vector field should have good properties such as
those of electrical fields. If we consider that the robot has
an electrical charge of the same sign as obstacles, then the
robot would be pushed away from obstacles. The properties
of this electric field are very good because it is smooth and
there are no singular points in the interest space.

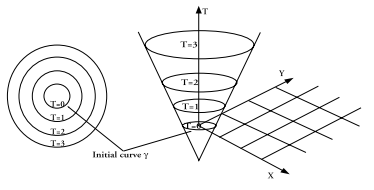
To help understand the Fast Marching Path Planning basis method, let us suppose a two dimensional wave propagating in a homogeneous medium. The front wave is then a circle propagating outwards the initial point. If an additional axis is added to represent the time, the results is as shown in the next figure:

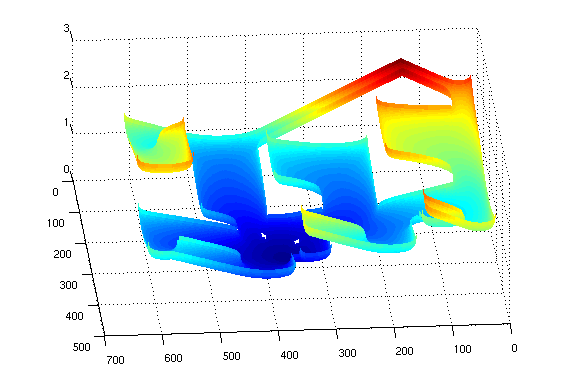
Now, if the initial point of the wave propagation are all those points which represents obstacles in a binary occupancy map, we obtain a map in which the value for each cell is proportional to the distance to the nearest obstacle, as shown in the next figures:

An the path obtained over this new “distances” map, applying the gradient method is:

FM2: Fast Marching Square

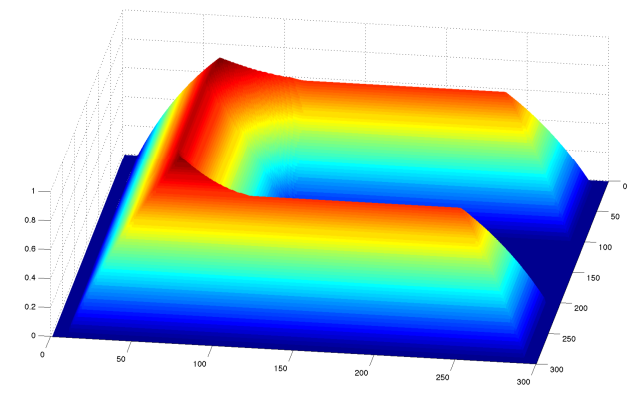
The path obtained applying Fast Marching directly is non-smooth and runs too close to obstacles, being not safe at all. The solution we propose is to use the “distances” map obtained applying Fast Marching as a slowness map. This means that the lower is the value for a given cell the closer it is to an obstacle (or wall) thus the velocity has to be slower.

Then, a wave is propagating from the goal point until it reaches the current position of the robot. For this propagation, the velocity of the wave for each cell is proportional to the value of the slowness map for that cell. Then it is obtained a map in which each cell has a value for the time the wave lasts to reach that cell. This map will never have local minima, since the velocity of the wave is always non negative.

The map with the time values applying Fast Marching over the previous slowness map is:

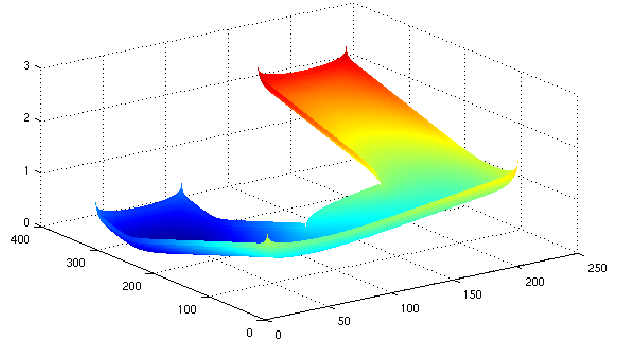
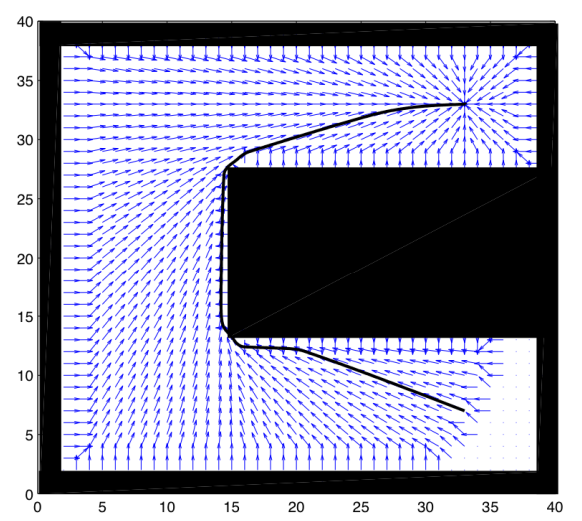
And applying the gradient method from the goal point to the initial point the path obtained is:

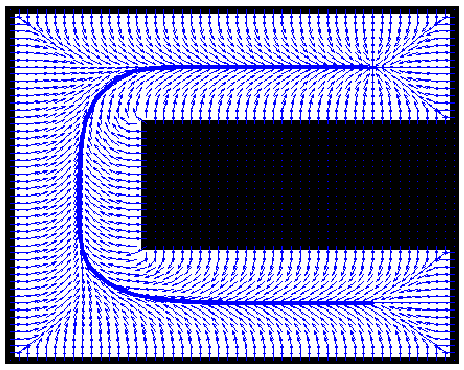
The result is a path much more smooth, safer and optimal in time.

We already proposed other alternatives such as Voronoi Fast Marching. Please, see the publications list below to find more information.

FM Applications

This proposed path planning has been applied successfully to:

– 2D and 3D path planning.
– Exploration and SLAM.
– Robot formations.
– Outdoor path planning.